Cosmic Romance

Curiosity is a peculiar trait which has been a foundational pillar of human civilization. Curiosity, which is ‘a strong desire to know or learn something’ can also be found in the animal kingdom. However the cognitive abilities of Homo sapiens have led us to dive deep into the unknowns of the world around us to extents far greater than any other animal. As soon as man’s belly was full with food and skin covered with clothes, he started looking up at the stars and wondered about it.

In this pursuit to know nature, Physics developed as a prime candidate. But soon man realized that to quantitatively understand and exploit nature, one needs a better language, a language in which one can talk to nature and listen to its calls. Mathematics as we know today, has been serving this purpose since. In the earliest days of advent of both of the disciplines, their motivations were mostly philosophical. Surely there were applications of what was developed, the pursuit of a purist was never that. Both Mathematics and Physics were developed hand in hand by thinker like Archimedes, Euclid and Pythagoras to Newton, Leibniz and Fermat. Their contributions to Math and Physics were never mutually exclusive. One was the motivation, while other the solution. However, with the advent of pure mathematical curiosity and the engineering aspects of Physics, there was a drift off between the two. Mathematics was seen by the mass as a mere tool for understanding the equations of physics and calculating the motion of ballistics, efficiencies of heat engines etc. and Physics became a mere application of Mathematics. Mathematically abstract concepts like imaginary numbers seemed to have no applications or even existence in the real world in which a Physicist was interested and Physics by that time became only solving differential equations.

This was a hard time for both the fields. They developed highly individually but, the spark seemed fading. But it wasn’t long when people realized that math is not just a mere tool. With Maxwell writing his electromagnetic equations in Mathematical form and Einstein using Riemannian Geometry to describe gravity, the fact that math and physics can’t be ripped apart, that they are intermingled was re-established, this time in a more firm manner.

And today, if one really wants to understand nature, mathematics can no longer just be treated as a ‘tool’. Mathematics has whole heartedly come up with all its branches from topology to functional analysis, from representation theory to number theory, to share its abstractness and wit with Physics. And Physics, like always has inspired Mathematics, reinforcing ideas and intuitions to the wild abstract minds of mathematicians. Though maths has its own abstract list of ideas, it never fails to amaze us how beautifully nearly all the instrumental ones fit to explain some aspect of nature. Physics and Mathematics hence seemed to have this intertwining cosmic romance from being born together to a seperated teenage to a more elegantly united adulthood. Afterall Pure Mathematics is, in its way, the poetry of logical ideas, where the muse is undoubtedly Physics!

A Brief History of Compactness

It was M. Fréchet who coined the term "compact" in a seminal paper leading to his 1906 doctoral thesis and gave definitions for what we now known as countable and sequential compactness.
On the otherhand, Alexandroff and Urysohn usually get credit for defining open-cover compactness.

The modern definitions (equivalent forms) of compactness are as follows:
Definition 1. A metric space (X, d) is said to be compact if it is totally bounded and complete.

Definition 2. A metric space (X, d) is said to be sequentially compact if every sequence in X has a convergent subsequence.

Definition 3. A metric space (X, d) is said to be compact if every open cover of X has a finite sub cover.

The origin of sequentially compactness is often trace to a theorem, proved rigorously by Weiestrass in 1877, which concern the behaviour of continuous functions defined on closed, bounded intervals of the real line. The following statement of the theorem comes from Fréchet who refereed it as a result of Weiestrass.

Theorem 4. Each function continuous in a limited (equivalent to modern day "closed and bounded") interval attains there at least once its maximum.

It seems that the motivation of defining sequential compactness in Fréchet's 1906 thesis came from his desire to generalize this theorem of Weiestrass to abstract topological spaces (E-spaces).

Interestingly, Weiestrass theorem owes its essential ideas from a result due to Bolzano which is now know as the greatest lower bound property for real numbers. In fact, the results of Bolzano allowed Weiestrass to prove that every bounded infinite set of real numbers has a limit point. It is this property that Fréchet actually used when he generalized Weiestrass theorem to abstract spaces. We now know this property as the Bolzano-Weiestrass property or limit point compactness.

While Bolzano and Weiestrass were trying to characterize properties of the real line in terms of sequences, other mathematicians, such as Borel, Lebesgue and Heine, were trying to characterize it in terms of open covers. The following theorem is now known as Heine-Borel theorem.

Theorem 5. A subset of ℝ is compact iff it is closed and bounded.

An other motivation behind compactness was the study of abstract topological spaces such as of space of continuous functions C[a, b]. It was noted that infinite dimensional spaces like C[a, b] were not as well behaved as finite dimensional spaces like ℝ or subsets of ℝ. For example, closed, bounded subsets of continuous functions on ℝ do not necessarily have the Bolzano-Weiestrass property or open covering property. The work along this direction is now known as Arzela-Ascoli theorem.

Theorem 6. A subset of C[a, b] is compact iff it is closed, bounded and equicontinuous.

A third motivation for the notion of compactness came from the quest to find solutions to differential equations. Peano (around 1890), a contemporary of Arzela and Ascoli realized that the Arzela-Ascoli theorem might be useful for demonstrating the existence of such solutions. He searched for solutions using sequential approximations what we now call compactness to show there will be a subsequence that converge to a limit (which will be the solution to the differential equation).

While it is not clear if Fréchet was aware of this application, it does seem to be the case that applications for the notion of compactness were known before the term was formally defined.

For further reading, one may refer to: [1] E. Hewitt: The role of compactness in analysis, The American Mathematical Monthly, Vol. 67, No. 6 (Jun. - Jul., 1960), pp. 499-516.
[2] MR Sundstrom: A pedagogical history of compactness, arXiv:1006.4131v2[math.HO] 2014.

Department of Applied Mathematics and Humanities,, S. V. National Institute of Technology, Surat, Gujarat, India - 395007.
E-mail address: gopaldhananjay@yahoo.in

Mathematics : A Journey

The question about the origin and use often strikes the mind of people who pursue Mathematics in their Higher studies. Many students start questioning this right from their "first year" and if not provided with a satisfactory answer, often "lose interest" in Mathematics. This behaviour is quite natural and in fact, a more precise word would be "human". Every newborn human is inquisitive in nature and is fascinated by how its surroundings work. When a child gets something new, the first thing it does is to smash it and look inside it. Although many parents classify this behaviour as "destructive", in science it is often referred to as "curiosity".

Speaking of curiosity, all the science we know today is a result of some curious brain. A famous and a cliche example would be Sir Issac Newton. Had Newton not been curious about why everything that goes "up" also comes "down" to the Earth, the field of Classical Mechanics and Calculus might be "invented" much later if not at all invented. We write the word "invented" in quotes for a special reason: People often ask, "Is Mathematics discovered or invented?"

To answer this question, we would probably have to go back more than 2000 years in history. Right from the time of Aristotle and Plato, philosophers (analogues of present day scientists) tried to understand the working of the universe in two major steps: First, they used to "observe" some phenomena and then try to "come up" with some explanation for this phenomena. As an example to this, Aristotle observed that when we push a block (or for that matter anything), it comes to rest after certain time. He gave an explanation that probably, the object (block, in this case) gets "tired" of moving and eventually rests. Although Aristotle could not explain how did this object get ``tired" of moving, centuries later this mystery was solved and it was called "Friction".

It was not long when we (humanity) could not explain phenomena by merely words. We needed a language which better communicated these physical phenomena. This is when we "devised" a language called "Mathematics". We carefully write "devised" instead of "discovered" or "invented" to avoid any controversies that may arise among the readers. Originally devised as a tool to understand physical phenomena alone, today the World of Mathematics has changed! Many Mathematicians have made a "division" which they call: Pure Mathematics and Applied Mathematics. While the "Pure" Mathematicians work with abstract concepts, the "Applied" Mathematicians try to fit in the abstract concepts into physical reality. It would not be surprising to hear that many "Pure" Mathematicians are too proud when their work does not fit into reality.

However, history is the evidence that most of these "Pure" Mathematicians have been wrong. Even a genius such as Hardy, who proudly claimed that his work (in Number Theory) would never be used in any real life application since it was "result of personal curiosity alone" was proved wrong when the work was used in population models and also by the military for communications. Therefore, it is safe to not distinguish work in Mathematics as "pure" or "applied". What may seem to have no application at present may gain some application even certain centuries later!

Coming to the original question about why do we "do" Mathematics. The answer is simple and yet to many laymen, it is non - satisfactory: We do it for feeding our own curiosities, to satisfy ourselves with answers to the questions that we raised. Everything boils down to understanding the universe which has been one of the goals of humanity for long. To achieve this goal, we have developed the language of Mathematics with certain syntax and grammar which we need to follow. It is a famous quote that if this universe was created by someone, then the creator must have been a Mathematician. And as Mathematicians, it is our responsibility to "decode" the universe in the terms it was written.

As a personal experience, many people have asked me (and even I have asked my teachers) about the "correct way" of "doing" Mathematics. The answer is that there is no "correct way". Instead, if we keep on asking questions about what we see and then try to find their solutions in a language the Nature understands, we are "doing" Mathematics "correctly". Our Education system (and this does not confine to the country alone) has taught us that the worst thing we can do is a "mistake". In research, this is not true! If we are afraid to make mistakes, we cannot make anything "new"; especially in a subject such as ours.

Why Programming

"I’m a pure mathematician, why should I learn to programme?"
"I am gonna be a theoretical physicist, better spend my time learning physics than coding!"
"I’m an experimental chemist, where would I use programming?"

If you think in line with the above statements then you are extremely wrong. Programming in the modern world is not just something reserved for specs-wearing-geeks sitting in front of a large screen punching in unlimited lines of code. It is open for all, rather I should say everyone must be open to programming. Look around you, the website on which you are reading this article, the applications on your smartphone, the recommendations that you get on e-commerce sites, all are made using programming. I’m not saying to leave your field of interest and jump on board to become a software developer. Rather, look for applications of programming in your field and if you can’t find any then you just aren’t looking hard enough.

You can also use programming in your daily life to automate trivial tasks. You could write a simple script to alert you when the price of your favourite shirt on amazon goes down, you could even autofill forms asking the same info again and again! If you somehow deal with data, then you can do wonders with programming in terms of effectively processing and analyzing your data. And if you ever plan in the future to go into the industry then programming is an absolute necessity without which (in 90% of the cases) you cannot even get an entry-level job!

If you are still not motivated enough to learn programming and think that it will be of no use to you in the future (I am hoping this is not the case!), let me give you one more reason. Whenever a programmer faces a problem or is given a new task, he doesn’t just start writing code. He breaks the problem into small parts, solves them separately and then goes into coding after making a planned structure for the entire problem. So, programming also helps to develop your problem-solving skills and, in the process, makes you more organized (if you are a programmer who follows community standards).

So, where and how to start learning? The biggest hurdle in learning programming is the inertia. To break that you have to put in some extra effort but once you start to gain interest there’s no looking back. So, my suggestion is to pick up Python (as it is beginner friendly), watch tutorials online, read books, join online courses or attend workshops and keep practising as much as you can. Remember that in programming the more experience you have the better you are.

Indian Contribution to Mathematics

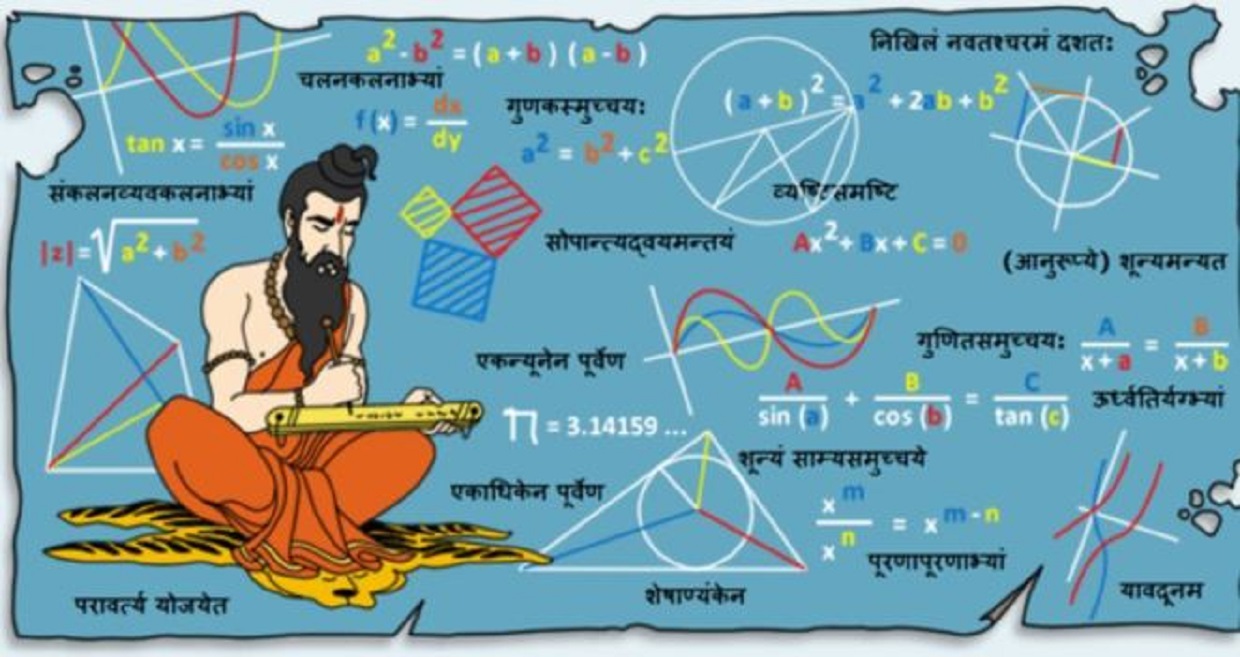
One look at the ruins of the ancient cities of Mohenjo-Daro and Harappa, and one is taken aback by the evident geometric sophistication and its practical implementation that went into planning the cities, considering that the Indus Valley civilization dates back to 2500-3000 BCE. Yet, the streets and city blocks are laid out in perfectly straight lines like in modern-day Manhattan. The concept of a place value system, and that of the number zero, which can function as a placeholder but has no value of its own, are so fundamental to our understanding and study of mathematics and seem so natural that we sometimes do not fully appreciate the brilliance in their simplicity. For the same, one simply needs to take but a glance at the Roman numeral system and the limited scope for computation that the cumbersome notations provide. For instance, the number 776 would be represented as DCCLXXVI in the Roman number system. Any further calculations upon the number using this notation would be virtually impossible. But these are just a couple of examples to assert the significance of the contributions made to mathematics by ancient and medieval Indian scholars. Over the years, Indian mathematicians made seminal contributions to the study of trigonometry, algebra, arithmetic, negative numbers and even advanced branches of mathematics such as calculus.

Despite such significant contributions to advanced fields of the subject, Indian contributions to mathematics have not been given due recognition, many feel, out of bias towards Western civilization, also termed as Eurocentrism. As stated by math historian G. G. Joseph,

"The awareness [of Indian and Arabic mathematics] is all too likely to be tempered with dismissive rejections of their importance compared to Greek mathematics. The contributions from other civilisations – most notably China and India, are perceived either as borrowers from Greek sources or having made only minor contributions to mainstream mathematical development. An openness to more recent research findings, especially in the case of Indian and Chinese mathematics, is sadly missing."

Hence, several discoveries that had earlier already been made by "oriental" thinkers much earlier than their European counterparts have been attributed to later mathematicians and scientists from the West. Let us take the example of the erroneously named Pythagoras theorem. Fields Medal winner and Princeton University Professor Dr Manjul Bhargava explained in an interview,

"The Pythagoras theorem should either be an Egyptian theorem if you look at the standard of just having an idea about it, an Indian theorem if you're looking for a complete statement of it, or a Chinese theorem if you're looking for the proof of it."

The Sulba-sutras (Sutra : rule or aphorism) date back to around 800 BC and are the earliest known mathematical texts in existence (though the mathematical knowledge recorded in these sutras is much more ancient). The Sulba-sutra of Baudhayana has the first recorded instance of an explicitly written theorem that states that if you have a right triangle, the square of the length of the hypotenuse is the sum of the squares of the lengths of the two legs. The purpose of these sutras was to aid in the construction of sacrificial altars and temples. The Buddhist Pagodas of South-east Aisa borrowed their plan of construction from the geometric grid of the Mandala (temples’ layouts) used for constructing temples in India. Furthermore, there is evidence of the knowledge of "Pythagorean" triplets for the construction of right angles, the knowledge of irrational numbers. Many rational and integral solutions of the Pythagorean equation a²+b²=c² were also quite well known to the Sulba geometers. For example, the triples (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (12, 35, 37) are explicitly used.

Apart from the knowledge, skill and ingenuity in geometry, the Vedic civilization was strong in the computational aspects of mathematics as well. Most of the standard results in basic arithmetic are of Indian origin. This includes neat, systematic and straightforward techniques of the fundamental arithmetic operations: addition, subtraction, multiplication, division, taking squares and cubes, and extracting square and cube roots; the rules of operations with fractions and surds; various rules on ratio and proportion like the rule and several commercial and related problems like income and expenditure, profit and loss, simple and compound interest, discount, partnership, computations of the average impurities of gold, speeds and distances, and the mixture and cistern problems similar to those found in modern texts. The Indian methods of performing long multiplications and divisions were introduced in Europe as late as the 14th century CE. One of the most remarkable statements found in the Sulba-sutras is the rational approximation of √2. The approximation is,

√2= 1 + ¹/₃ + ¹/₍₃₎₍₄₎ - ¹⁄_((3)(4)(34)) , which gives a value correct up to 5 decimal places.

The decimal notation and the idea of place value developed in India allowed mathematicians and scholars to handle large numbers right from the Vedic ages (1500 – 500 BCE). There is terminology for all multiples of 10 up to 1018 in Vedic literature, and the Ramayana has terms all the way up to 1055. In contrast, their Greek counterparts only had terminology for numbers up to 104, and the Roman numerals didn’t exceed 103 in value. Due to the absence of such an effective number system that could help represent such large numbers, among other factors, after a Golden period of mathematics in Greece (600 BCE – 300 CE), creative mathematics saw an eventual decline there. The Indian notation and arithmetic eventually got standardised in Europe only during the 16th and 17th century, when the Arabs brought the "Hindu-Arabic" numerals to the continent. Not just the decimal system, even a form of binary system had been pioneered by Indians of the time. The Indian scholar Pingala (c. 2nd century BC) developed a binary system for describing rhythmic structure of verses; he used binary numbers in the form of short and long syllables. They were known as laghu (light) and guru (heavy) syllables.

On the other hand, growth of Indian mathematics saw no such decline during the first millennium after Christ. Quite the contrary, the period saw the rise of astrologer/astronomer-mathematicians in the subcontinent, which include big names such as Aryabhata I, Varahamihira, Brahmagupta, Aryabhata II, Bhaskara II, MCEhava of Sangamagrama and Nilakantha Somayaji, and other mathematicians such as Bhaskara I, Shridhara, Mahavira, etc. and they ushered in the Golden age of Indian mathematics (400-1600 CE). In fact, mathematics of that period was included in the 'astral science' (jyotiḥśāstra) and consisted of three sub-disciplines: mathematical sciences (gaṇita or tantra), horoscope astrology (horā or jātaka) and divination (saṃhitā).

The majority of development of algebra in the subcontinent occurred during these very ages at the hands of these early advocates of algebra. Its purpose was to aid in complex astronomical calculations that involve many variables, for the derivation of unknown quantities. Algebra is a short-hand method of calculation and by this feature it scored over conventional arithmetic for this application. Conventional mathematics in India was called Ganitam, and this "new" field came to be known as Bijaganitam, or literally the "other" mathematics. It originated in India around 5th century CE and has been referred to by Aryabhata I (476 – 550 CE) in his treatise, Aryabhatiya. The advancement of studies in the subject meant that Indians could take their mathematical concepts to an abstract plane and with the aid of a simple numerical notation devise a rudimentary algebra as against the Greeks or the ancient Egyptians who due to their concern with the immediate measurement of physical objects remained confined to mensuration and geometry. This system of mathematics in India was adapted by the Arabs and given the name ‘Al-Jabr’ meaning ‘the reunion of broken parts’. ‘Al’ means ‘The’ & ‘Jabr’ means ‘Reunion’. This name given by the Arabs indicates that they took it from an external source and amalgamated it with their concepts about mathematics.

The systematic use of symbols to denote unknown quantities and arithmetic operations was pioneered by these astronomer-mathematicians. The four arithmetic operations were denoted by "yu", "ksh" "gu" and "bha" which are the first letters (or a little modification) of the corresponding Sanskrit words yuta (addition), ksaya (subtraction), guna (multiplication) and bhaga (division); similarly "ka" was used for karani (root), while the first letters of the names of different colours were used to denote different unknown variables. The Indians classified and made a detailed study of equations (which were called sami-karana), introduced negative numbers together with the rules for arithmetic operations involving zero and negative numbers, discovered results on surds, described solutions of linear and quadratic equations, gave formulae for arithmetic and geometric progression as well as identities involving summation of finite series, and applied several useful results on permutation and combinations including the formulae for ⁿP_r and ⁿC_r.

The treatise Aryabhatiya contained invaluable work on the solutions of simultaneous quadratic equations, whole number solutions of linear equations and on the general solution of the indeterminate linear equation. Brahmagupta, in his astronomical work, Brāhma Sphuṭa Siddhānta (628 CE) also wrote two chapters devoted to topics such as cube roots, fractions, ratios and proportions, barter, mathematics for practical purposes, his famous theorem on the diagonals of a cyclic quadrilateral, as well as the first explicit solution (not completely general) of equations of the form,

ax²+ bx = c

It went, "to the absolute number multiplied by four times the [coefficient of the] square, add the square of the [coefficient of the] middle term; the square root of the same, less the [coefficient of the] middle term, being divided by twice the [coefficient of the] square is the value." This is equivalent to:

x= (√(4ac + b²) - b)/2a

Brahmagupta used the ideas of 'fortunes' and 'debts' for positive and negative numbers. Brahmagupta used a special sign for negatives and stated the rules for dealing with positive and negative quantities; for instance,

"A debt minus zero is a debt.
A fortune minus zero is a fortune."

Brahmagupta was also able to make progress in finding (integral) solutions of Pell's equation, x²-Ny²=1 and in particular he showed how to obtain solutions starting from an integer solution of the equation x²-Ny²=k for k = ±1, ±2, or ±4. In his commentary, Brahmagupta posed a particular case of the problem, with N=92, and remarked "a person solving this problem within a year is a mathematician." Sridharacharya (750 CE) gave the well-known method of solving a quadratic equation by completing the square: an idea with far-reaching consequences in mathematics. The Pascal's triangle for quick computation of ⁿC_r is described by Halayudha in the 10th century CE as Meru-Prastara 700 years before it was stated by Pascal.

The Surya Siddhanta is the name of a Sanskrit treatise in Indian astronomy from the late 4th-century or early 5th-century CE. The text survives in several versions, was cited and extensively quoted in a 6th-century CE text by Varahamihira.

Quick snippet: Varahamihira was earlier known only as Mihira, and the title of Varaha and the royal ensign of the varaha or boar was conferred onto Mihira when he accurately predicted the date and time of the death of Emperor Vikramaditya’s son and heir apparent to the throne.

This remarkable ancient text estimates the length of an Earth year, the diameters of the planets with an accuracy hard to fathom for that day and age, and describes the motion of the planets.

"Objects fall on earth due to a force of attraction by the earth. therefore, the earth, the planets, constellations, the moon and the sun are held in orbit due to this attraction",
it is mentioned in the Surya Siddhanta. It was not until the late 17th century in 1687, that Isaac Newton rediscovered the Law of Gravity. Surya Siddhanta also contains the roots of modern trigonometry. It uses sine (jya), cosine (kojya or "perpendicular sine") and inverse sine (otkram jya) for the first time, and also contains the earliest use of the tangent and secant when discussing the shadow cast by the gnomon of a sundial. Although the Greeks are credited with the founding of the subject of trigonometry, their progress was halted due to the absence of adequate algebraic machinery and notations. Indians not only invented the sine and cosine functions, but discovered most of the standard formulae and identities, and constructed accurate sine tables. Remarkable approximations for π (‘pi’) are given in Indian texts including 3.1416 of Aryabhata (499 CE), 3.14159265359 of Madhava (14th century CE) and 355/113 of Nilakanta (1500 CE).

A very celebrated and essentially the last of the classical age (400 – 1200 CE) mathematicians in India, whose name deserves special mention, was Bhaskaracharya or Bhaskara II. His work Siddhanta-siromani is divided into four parts: Leelavati (contains problems on arithmetic, permutations and combinations, geometry, quadratic equations), Bijaganita (Algebra), Grahaganita (Astronomy) and Goladhyaya (study of the celestial sphere). The first part is said to be named after his daughter who became a widow at an early age and the work Leelavati was written by Bhaskara to console her. He provided methods to find solutions of quadratic and cubic equations and worked on solutions of equations with more than one unknown. He devised, along with Jayadeva (~ 950 – 1000 CE), the chakravala method to find the general solution of Pell’s equation and the general indeterminate quadratic equation, among other works. He had also contributed to other fields, including geometry, trigonometry, calculus, astronomy. He satisfactorily proved the Pythagoras theorem. But the most remarkable of his works has to be that on calculus, wherein he had already discovered many of Gottfried Leibniz’s ideas 500 years before he started his own work in the 17th century on the development of calculus, that forms the basis for the study of subject in the modern day. Bhaskara was familiar with the notion of integration as a limit of finite sums. For instance, he calculates the surface area of the sphere, by dividing it into annuli and drawing a system of parallel circles, or by dividing the surface into lunes by drawing meridian circles through a pair antipodal points on the sphere and dissecting each lune into a large number of small quadrilaterals by drawing circles parallel to the equator. Bhaskara also had ideas about differentiation in connection with the so called instantaneous method (tatkalika) by dividing the day into a large number of small intervals and comparing the positions of the planet at the end of successive intervals. Bhaskara also knew the addition formulae for the sine function,

sin⁡(α ± β)=sin⁡α cos⁡β ± cos⁡α sin⁡β, and contributed to spherical trigonometry.

The Kerala school of astronomy and mathematics, founded by Madhava of Sangamagrama in the 1300s, was responsible for many firsts in mathematics, including the use of mathematical induction and some early calculus-related results. In attempting to solve astronomical problems, the Kerala school astronomers independently created a number of important mathematics concepts. The most important results, series expansion for trigonometric functions, were given in Sanskrit verse in a book by Neelakanta called Tantrasangraha and a commentary on this work called Tantrasangraha-vakhya of unknown authorship. The theorems were stated without proof, but proofs for the series for sine, cosine, and inverse tangent were provided a century later in the work Yuktibhāṣā (1500 – 1610 CE), written in Malayalam, by Jyesthadeva. The discovery of these series expansions was undoubtedly an achievement, but the Kerala school cannot be said to have developed calculus. While they were able to develop Taylor series expansions for the important trigonometric functions, differentiation, term by term integration, convergence tests, iterative methods for solutions of non-linear equations, and the theory that the area under a curve is its integral, they developed neither a theory of differentiation or integration, nor the fundamental theorem of calculus.

In conclusion, one can safely state that it is on the foundation formed by the blending of the two great mathematical cultures - the geometric and axiomatic tradition of the Greeks and the algebraic and computational tradition of the Indians - that the mathematical renaissance took place in Europe during the 17th to 19th century period. It is definitely still to the credit of these late European mathematicians to have started from scratch and re-developed the branches of mathematics whose knowledge was, in effect, lost until rediscovery and/or reinterpretation of these precious texts in modern times. The same was made difficult, in part, by of the complicated verse format of the Sutras. They could not be deciphered unless through extensive commentaries by certain distinguished teachers belonging to later traditional schools of learning based on the gurukula system. It’s unfortunate that Indians took virtually no part in the re-birth of mathematics from the 17th century onwards, and so, while high-school mathematics, especially in arithmetic and algebra, is mostly of Indian origin, one rarely comes across Indian names in college and university courses as most of that mathematics was created during the period ranging from late 17th to early 20th century. In modern times again, there has been a resurgence of Indian mathematics; several Indian mathematicians have done remarkable work in different fields of mathematics and made significant breakthroughs. Some of the biggest names that come to the mind are those of Srinivasa Ramanujan, Prashanta Chandra Mahalanobis, Dr Harish Chandra, Manjul Bhargava and C.R. Rao. However, their work far exceeds the scope of university curricula and not too many students get to learn about their contributions first-hand.

The point that the article intends to drive home is that there has been a rich culture of mathematical research in the subcontinent since the Vedic times. It is about time that the important role of India in the development of the subject is given the due recognition that it deserves.

Abel Prize

About the Abel Prize
The Abel prize was established by the Norwegian government in 2002 on the occasion of the 200th birth anniversary of Niels Henrik Abel (1802-1829). Despite of his short life, he made significant contributions to a variety of mathematical fields and hence named after this great Norwegian mathematician, the Abel Prize have often been described as " Mathematician’s Nobel Prize". The laureates are selected by the Abel Committee, the members of which are appointed by the Norwegian Academy of Science and Letters.

The Abel Prize recognizes contributions to the field of mathematics that are of extraordinary depth and influence. The prize comes with a monetary award of 6 million Norwegian krone (approximately €620,000 or $700,000) and has been awarded annually since 2003. In addition to honouring outstanding mathematicians, the Abel prize shall contribute towards raising the status of mathematics in society and stimulating the interest of children and young people in mathematics.

First Women to win The Abel Prize
On Tuesday, 19 March 2019, Karen Uhlenbeck became the first woman to win the Abel Prize since its inception in 2003. His Majesty King Harald V will present the Abel Prize to the laureate at the award ceremony on the 21st May in Oslo. The lady from United States is a professor emeritus of mathematics at the University of Texas at Austin. She is also a visiting senior research scholar at Princeton University and a visiting associate at the Institute for Advanced Study (IAS). According to her IAS profile her current research interests include "flat complex connections and moduli spaces of geometric structures on complex connections." She was recognized for her pioneering achievements in geometric partial differential equation, gauge theory and integrable systems, and for the fundamental impact of her work on analysis, geometry and mathematical physics. "Her theories have revolutionized our understanding of minimal surfaces, such as more general minimisation problems in higher dimensions", stated Hans Munthe-Kaas, who chairs the award committee. Her work is also described as one of the most important in the field of mathematics in the 20th century. Uhlenbeck once described her eye-catching type of questions that lead her to ponder in astonishment about the question to be viewed differently. "It’s a combination of being fairly concrete - so one can understand concretely examples – and also connecting with a lot of other ideas. For example, you see the analysis in a minimal surface equation, but then you also realize it has connections with other geometric questions that are not just analysis. I am definitely very attracted to the idea that there are a lot of different facets in mathematics and seeing the connections," Uhlenbeck said.

It is evident that her research has led to revolutionary advances at the intersection of mathematics and physics in such a way that seems unreal. "Her pioneering insights have applications across a range of fascinating subjects, from string theory, which may help explain the nature of reality, to the geometry of space-time." stated Paul Goldbart, dean of the College of Natural Sciences at the University of Texas at Austin. Other than a respectable mathematician, Karen Uhlenbeck is also one of the co-founder of IAS Women and Mathematics (WAM) program. "WAM encourages female mathematicians to form collaborative research relationships and to become active in a vertical mentoring network spanning a continuum from undergraduates to emerita professors, which provides support and reduces the sense of isolation experienced by many women in mathematics," the website for that program notes, adding "While there are a number of women’s programs targeted solely at undergraduates or graduate students, or postdocs, very few programs provide the depth and breadth that come from simultaneously including features tailored for undergraduate students, graduate students, and researchers from a board spectrum of US institutions, all in one united community of scholars, as WAM does." Her other awards include the University of Michigan alumna of the year (1984), the sigma Xi Common Wealth for Science and Technology (1995), and honorary doctorates from the University of Illinois at Urbana-Champaign (2000), Ohio State University (2001), University of Michigan (2004), Harvard University (2007) and Princeton University (2012).

What Students Teach Us

Disclaimer: The ideas presented in this article are purely personal and not motivated by any group or institution. Although, I hope my colleagues will agree to some (if not all) of the points I make here, I deeply regret any dissent that may arise.

My title does not include a modal auxiliary "can" as I write based on my experience of teaching over a decade. In my teaching career, while I taught according to the syllabi, my students in all their innocence, involuntarily taught me arbitrary things.

I go against the popular adage that students learn from teachers, as I feel teachers also learn some real life lessons from their students. Sometimes wisdom comes before age (Read before you turn 40).

Students, I think have a gifted ability (sometimes inherent and sometimes trained) to listen. The fact that they continuously listen for at least 6-7 hours a day develops their listening ability. As teachers we are accustomed to delivering talks sometimes for hours at a stretch. We even take pride in the way we share our thoughts and teach our pupil. But ask us to sit and listen for one whole day without questioning/ interrupting/ evaluating/ paraphrasing or rejecting the speaker and you will understand how swiftly we have lost the ability to listen without judging others. As we grow and claim our expertise in certain fields, we speak more and listen less. Especially when the listener is half our age, we preordain and assume his/ her ability. Hence, let's learn the skill of listening from our students, as listening in an effortless and energy saving way to gain knowledge and acquire varied perception on things. Secondly, students especially the ones who passively listen to their teachers and lack confidence or determination to question, ironically, teach an interesting lesson without words. Call it their love for the comfortable benches or "why bother to speak" attitude, they sit through our class but speak to us only through their ability to communicate non-verbally. They teach us the art of questioning, doubting, disagreeing, misunderstanding, agreeing and confusing and many more through their facial expressions. Our classroom is an presents a vast platform to learn body language. Once observed carefully, we can pick the emotions enlisted above simply by the way muscles alter on our students’ faces. Hence without even uttering a word they assiduously convey their thoughts. An art that can come in very handy in meetings where without saying many emotions can be conveyed. Call it diplomacy or effective communication, it can be a valuable tool.

In Steven Covey's celebrated book, 7 Habits of Highly Effective People he gives "Putting first thing first" as the 3rd habit that effective people have. I understood its effectiveness not when I read the book, but when I closely observed many students who were focused and goal oriented. A simple example- when we teach them we are often made to feel like we are their favourite teacher, in the very next class the same assurance is provided to the other teacher. Initially, I saw it as a sign of opportunism but I gradually picked the signs of focus and determination of students to live in the present. Now, I have learnt to give full attention and importance to everyone who I interact with. Thus, I learnt "The Power of Now", not from Eckhart Tolle who theoretically explained it in his famous book, but from my dear students.

Who can teach us risk taking better than the fearless and optimistic youth that energises our class rooms? Yes, risk taking and adventure are definitive traits of the young. Emphasising the same Samuel Taylor Coleridge in his poem Youth and Age wrote, "That ask no aid of sail or oar, that fear no spite of wind or weather, nought cared this body for wind or weather, when youth and I lived isn’t together." Honestly speaking, sometimes I envy the ease and fearless will with which our young students embark on any new assignment. They are always willing and keen to experience that which is unknown. My heart fills with admiration and sorrow at once when I see the confidence to scale greater heights in them. It reminds me of the caution and inhibitions that hinder my spirit to soar like them.

Of all the enlisted lessons, the most valuable lesson that I learnt and hope to continue learning is the effective use of technology. I can proudly state, through many discussions and presentations of my students, I learnt the use of Dropbox, Evernote, Text Fairy, in shorts, Google docs etc. The pace at which technology intervenes our lives, can be intimidating for some of us. Hence, in order to follow close behind, if not match steps with technology, I have learnt to seek advice of the youth who have been empowered by it. Masters in hacking, ethical or otherwise, agents of pirated data, the geeks in the class are often an institution of technology. Diligently persistent these students can tutor us on internet and the world of possibilities.

Another great lesson my students taught me was the zeal to learn. Psychology says a child learns the most till he/ she is 5 years old and the cognitive abilities decrease with age. In their early twenties, I see students keen and desperate to learn. With their understanding fully developed, these post teens youth that inhabit our class rooms are eager to learn. Science students will curiously follow a story and engineering students will listen to critical appreciation of a poem to understand the emotions. Hence subjects, courses and disciplines are our narratives forced on them. They come to a place of learning, seeking knowledge, we put them in water tight compartments or boxes of science, commerce, engineering, arts etc. Their attitude toward learning reminds me of the interdisciplinary nature of knowledge, and how unless we learn to co- relate things our education remains incomplete.

I also perceive a stoic "never-give-up" attitude in our students. When they face hardships and challenges, mainly caused by the limitations in their school education, they fight these obstacles and conquer their limitations with unimaginable zest and courage. With great admiration I admit, most of our students show us the true essence of life. I witnessed the weakest of weak students re-write their growth trajectory, which validates my belief in "never- give- up" mantra.

I might be sounding very flattering throughout. So let's talk about things we don't like, but yet, our students teach us. Winston Churchill once said, "Personally I'm always ready to learn, although I do not always like being taught." On a similar note our students teach us the incomprehensible ability to be sorted in a mess or let's put it differently - being organised in thoughts and unorganised in life. Some students find their creative faculties charged while living a chaotic routine. They defy our age old belief in pattern, patience and perfection. They successfully master the art of instant accomplishment and instant gratification. Their last minute submissions and requests force us into such indulgence.

Last but not the least (because I hope I will continue to learn many new things) is the skills of effortless communication which is ubiquitous thanks to internet. Initially it was called "SMS language" now popularly known as text language, it overlooks all rules of language learning and has led to the transformation of communicative language at an exponential rate. LOL, B4N, CU, L8R which surrounds us are the basics of effective communication which every student naturally uses. These "textese" are not taught, they are acquired because of common usage. While centuries old bards and grammarians may be tossing and turning in their graves, these millennial take liberties of language and write without bothering about spelling or grammar. Surprisingly, their message is conveyed faster, is often witty and is universally understood. Although it might cause an occupational crisis in the lives of English teachers, let's not live in denial, textese is the language of fast communication in this fast paced world. I accept this aberration of language as I follow what Aristotle once said, "It is the mark of an educated mind to be able to entertain a thought without accepting it." Hence, I might not accept it whole heartedly, but I am learning the text language from my students.

Multitasking may be a millennial fashion, but it is worth learning. "Jack of all trade and master of none" is no longer an idiom used to depict a flaw. Seeing my students master many skills at a time, I wonder if expertise in one vocation a fallacy these days? Nevertheless, with expectations, responsibilities and competitions multiplying, multitasking is a task worth taxing ourselves over.

To conclude, I dedicate this piece to my students who have inadvertently taught me many things but I also want them to always remember that learning is an everlasting process and the day you cease to learn you cease to grow. Also, you may have taught me these lessons involuntarily but if, you decide to teach voluntarily (i.e. become a teacher), do it because you passionately wanted to. To quote Aristotle, "Teaching is the highest form of understanding." Therefore, teach if you wish to learn and convey with joy, what you have learnt.

IntERAct : Internship Experience and Research Activities seminar

About IntERAct
The IntERAct seminar series was initiated by Integrated M.Sc. students. The seminars are conducted by students for their juniors. In this, the students who have completed internships or have achieved something new share their experience and knowledge to others.This programme is beneficial for both listeners as well as speakers.The listeners gain exposure, and learn about various fields of work, while the speakers learn to address crowds with confidence. It is always great to speak to people our age, who understand the situations we go through, and they can guide us better. IntERact provides a platform for this purpose,and remains one of the best initiatives ever undertaken by M.Sc. Students.

Here is some information about seminars held in previous years:

• 3rd August, 2017: Data Analysis
  The seminar was given by Ms. Manpreet Budhraja. She had done her internship in Essar steel on data analysis. She shared her experience and talked about the basics of data analysis.
  
  
• 9th August, 2017: The key to Cryptography
  This seminar was given by Mr. Sarthak Gupta. In the seminar he talked about the importance of number theory in cryptography.He also discussed modular arithmetic, encryption- decryption and their applications.
  
  
• 16th August, 2017: Computations with B-splines
  The seminar was taken by Mr. Sourav Majumdar. The topic he chose is from numerical analysis.
  
  
• 21st August, 2017: Abstract Algebra
  The seminar was delivered by Ms. Gowri Chandran. She had done her internship from IISER Mohali. She emphasized on properties of groups, rings and fields and then talked about various sources from which we can extend our horizons in abstract algebra.
  
  
• 30th August, 2017: Tools and Techniues of Analysis
  The speaker was Mr. Aniruddha Deshmukh. He discussed the uses of quantifiers,logic,sets boundedness and properties of real numbers.
  
  
• 5th September,2017: Natural Language Processing
  This seminar was given by Mr. Vaibhav Maheshwari. He talked about natural language processing and how it is evolving in the current scenario.
  
  
• 27th September, 2017: Secetary Problems
  The seminar was delivered by Ms. Supriya Murdia and her topic of interest was The Secetary problem. It is an application of the optimal stopping theory and is widely studied in probability and statistics and decision theory.
  
  
• 1st November, 2017: Fuzzy Set Theory and T Norms
  The seminar was given by Mr. Kavit Nanavati. In the seminar he briefed the audience about fuzzy sets and related notations.
  
  
• 8th November, 2017: Inventory Methods using Heuristic Approach
  This seminar was delivered by Mr. Rakesh Das.
  
  
• 16th November, 2017: Integral Transforms
  The seminar was given by Mr. Nagesh Sahu. In the seminar he talked about different types of integral transforms and its applications.
  
  
• 10th January, 2018: Analytics
  The speaker in this seminar was Ms. Kanchan Kushwaha. In the seminar she talked about basics of analytics, statistics, case studies and career in analytics.
  
  .
• 17th January, 2018: Data Assimilation
  The seminar was taken by Mr. Abhishek Shah. In this seminar he gave insights about data assimilation, different methods of data assimilation, and it's applications.
  
  
• 31st January, 2018: Fundamentals
  In this session of IntERAct Mr. Sarthak Gupta took a workshop on the fundamentals of mathematics. This session was a very challenging, yet fun one.
  
  
• 7th February 2018: Mathematical tools for Advanced Linear Algebra
  The seminar was given by Mr. Ram Kumar. He discussed about vector spaces, Hilbert spaces, dirac notations, inner product, properties of kets and bras, operators and transformations and uncertainty principle through operators.
  
  
• 29th August, 2018: Inner product, Norm & Metric.
  The seminar was conducted by Mr. Aniruddha Deshmukh. He discussed the relation between vector inner product, norm and metric. He also explained the new concept of "p-adic" metric for vector space of rational numbers.
  
  
• 11th September,2018: Machine Learning
  The seminar was conducted by Mr. Aman Bakshi. He introduced the audience to the concept of artificial intelligence and machine learning which is a trending topic these days. He also gave insights about neural networks.
  
  
• 16th October, 2018: Nature of Exponential Function
  This seminar was delivered by Mr. Shubham Yadav. He talked about the exponential function and how calculus helps to manifest function through definitions. He talked about the unnatural definitions of exponential function.
  
  
• 23rd October, 2018: Cryptography and Information Security
  This seminar was conducted by Ms. Gowri R Chandan. She talked about cryptography and its application in information security. She gave us insights about various ways of encryption, authentication and related information about cyber security.
  
  
• 30th October, 2018: Travelling Salesman Problem
  The seminar was given by Mr. Harsh Jariwala. He talked about the aforementioned problem, solution methodology and application of the traveling salesman problem.
  
  
• 30th January, 2019: Perturbation technique on Eigen Value Function
  The seminar was conducted by Mr. Ram Kumar. He has tried to find out the approximate solution of an eigen value problem using the concepts of asymptotic iterations and Ricatti’s criterion.
  
  
• 6th February 2019: Mathematics behind Machine Learning
  The seminar was conducted by Mr. Samridh Khaneja. He briefly discussed about types of machine learning, basic terms and simple models which were designed using mathematical and statistical tools.
  
  
• 13th February 2019: Problem related to Prime Numbers
  This seminar was conducted by Mr. Sarthak Gupta. He shared his experience about formulating the problem and how he was able to solve it using different tools.
  
  
• 27th March, 2019: Subspaces of Plane and Space
  The seminar was delivered by Mr. Vishal Agarwal. He discussed classes of subspaces of plane and space and gave an elementary proof that there cannot be any other class. He gave all the linear subspaces which we can have in plane and space.
  
  
• 3rd April, 2019: Schroder-Bernstein Theorem
  The seminar was given by Mr. Ashwin Verma. He proved Schroder-Berstein theorem very elegantly and in organized manner. The theorem is about constructing bijection between two sets. He gave us the application of this important theorem.
  
  
• 10th April, 2019: Non-Euclidean Spaces on Rⁿ
  The seminar was delivered by Mr. Shubham Yadav. He introduced the notion of dimension of a space. He also discussed about what should be the dimension of what we call the n-space Rⁿ. Then he showed how the dimension of any space depends upon the algebraic structure.
  
  

Overall, the IntERact seminars conducted so far have been a great success, and we are confident that students will continue them with full enthusiasm.

Achievements of Our Students

Awards
-Mr. Rakesh Das won the best paper presentation award. The paper was presented at International conference of FORBS 2018 organized by Calcutta Business school in collaboration with Operational Research Society of India, Kolkata chapter.

Research article
-Mr. Sarthak Gupta published his first article about a problem related to number theory in "The Mathematics Student".

Internship
-Mr. Vaibhav Jaydeo Khobragade and Mr. Garvit Bhatt were interns at Melzo Company, Surat. Their internship was about "Business Development"
-Ms. Ekta Jain, Mr. Sahil Unagar and Mr. Aman Bakshi were selected as summer interns by Indian Academy of Sciences.
-Mr. Samridh Khaneja, Mr. Mahipal Upadhyay and Mr. Dhruvrajsinh Omkarsinh Vansia were selected for Summer intership in SVNIT-Surat

Competitions
-Mr. Ravi Kiran Paila cleared CSIR - NET LS in June 2018
-Mr. Kavit Nanavati , Mr. Harshad Sakariya, Ms. Jyoti Yadav and Mr. Parth Sartanpara cleared GATE with AIR 304, 534, 899 and 1120 respectively.
-Ms. Prakruti Kalsaria, Mr. Akash Patel, Mr. Ankit Sharma, Mr. Saubhagya Tripathi and Mr. Harshil Pathak became the toppers from Gujarat & Rajasthan of Madhava Mathematics Competition-2019 with rank 2, 3, 6, 8 and 17 respectively.
-NET exam in Mathematical Sciences in dec 2018 was cleared by Mr. Shubham Yadav, Mr. Rahul Kamble and Mr. Kavit Nanavati with JRF AIR-75, LS AIR-120 and JRF AIR-107.

Trainings
- Mr. Lavuri Devilal attended Mini MTTS held at Vijayawada, Andhra Pradesh
-Mr. Anirudhha Deshmukh attended MTTS training held at IISER Thiruvananthapuram. He had been selected three times in a row for this influential training.
-Ms. Ishika Bhatt was selected for the Summer School on Mathematical Finance at Chennai Mathematical Institute.
-Mr. Akash Patel, Mr. Ankit Sharma, Mr. Saubhagya Tripathi, Mr. Harshil Pathak, Mr. Ashwany Verma, Ms. Prakruti Kalsaria and Ms. Priya Singh attended the P. C. Vaidya Second Summer School in Advanced Mathematics.
-Mr. Akash Patel, Mr. Ankit Sharma and Ms. Prakruti Kalsaria attended Madhava Nuture Camp 2019 at St. Xavier’s College, Ahmedabad.

Scholarship
-Mr. Rutvij Tole, Ms. Shreya Sheladia and Mr. Aniruddha Deshmukh were awarded the INSPIRE - SHE. They will be receiving 80k per year till completion of their Master's degree.

In the memory of George Finlay Simmons

"George Finlay Simmons" is a name not really much known outside the world of Mathematics. Even if we search for this name on Google, we wouldn't really find a lot of information. What we would find however, are the names of the numerous books written by him.

For those who are reading this name for the first time, he was an American mathematician and the author of some books that tried bought a fresh perspective to the field of mathematics. He actually considered existing textbooks as "dreadful" and started fixing the situation with a series of his own texts.

He started with the book "Introduction to Topology and Modern Analysis" (1963) and ended with "Calculus Gems" (1992). To him, mathematics was not something that had to be done solely and entirely without connection to other subjects or fields. He was no fan of the 'block plan'- in which students had to work on a single subject for a long amount of time with a complete disregard of other subjects.

As he stated, "Mathematical rigor is like clothing; in its style it ought to suit the occasion, and it diminishes comfort and restricts freedom of movement if it is either too loose or too tight."

He worked in many universities and colleges in his lifetime, including Williams College, the University of Rhode Island, Yale University, the University of Maine, and the University of Chicago.His main area of mathematical work was Topology and classical analysis.

On 6th August 2019 he took his last breath, and the world lost another "Poet of patterns". We will always be grateful for his many contributions. We salute his spirit, and pay our respects to a true man of ideas, a true man of Mathematics, a man of true principles.